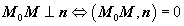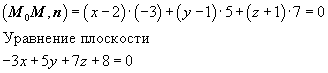№ 1

 Составить уравнение плоскости, которая проходит через точку 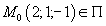 и имеет вектор нормали  .

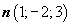Решение

 Возьмём текущую точку на плоскости  .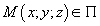

Вектор 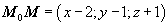 принадлежит плоскости П. Поскольку этот вектор перпендикулярен вектору нормали, то

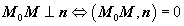
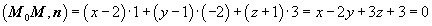
Уравнение плоскости:

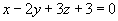
№ 2

 Составить уравнение плоскости, которая проходит через точку 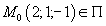 параллельно плоскости .

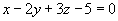Решение

Плоскость 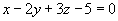 имеет вектор нормали  n(1; -2; 3) - это коэффициенты при переменных  x, y и z в уравнении данной плоскости. Т.к. плоскости параллельны, то их векторы нормалей коллинеарны. За вектор нормали искомой плоскости можно взять вектор нормали данной плоскости. 

 Возьмём текущую точку на плоскости  .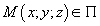

Вектор 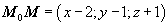 принадлежит плоскости П. Поскольку этот вектор перпендикулярен вектору нормали, то

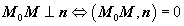
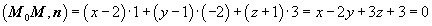
Уравнение плоскости:

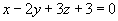
№ 3

 Составить уравнение плоскости, которая проходит через точку 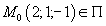 перпендикулярно прямой  . 

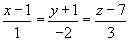Решение

В качестве вектора нормали искомой плоскости можно взять направляющий вектор данной прямой a. Координаты напрявляющего вектора прямой являются знаменателями в канонической форме записи уравнений прямой. Поэтому,  n = a = (1; -2; 3). 

 Возьмём текущую точку на плоскости  .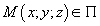

Вектор 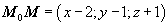 принадлежит плоскости П. Поскольку этот вектор перпендикулярен вектору нормали, то

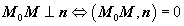
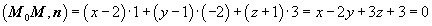
Уравнение плоскости:

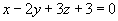
№ 4

Составить уравнение плоскости, которая проходит через точку 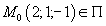перпендикулярно двум данным плоскостям 

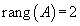
Решение

Возьмём текущую точку на плоскости  .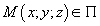

Вектор 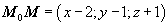 принадлежит плоскости П. 

Поскольку этот вектор перпендикулярен вектору нормали, то

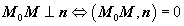
Т.к. искомая плоскость перпендикулярна обеим заданным плоскостям, то за вектор нормали n  можно взять направляющий вектор прямой, полученной в результате их пересечения.

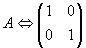
Возьмём текущую точку на плоскости  .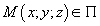

Вектор 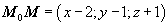 принадлежит плоскости П. Поскольку этот вектор перпендикулярен вектору нормали, то